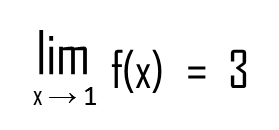Limits Demystified (Part 2)

Welcome back! If you’ve read my last post Limits Demystified (Part 1) I hope you realized that calculus isn’t that scary. In fact, according to my personal experience, limits are in fact easier to comprehend than many Algebra 1 topics. Absurd but realistic.

Limits Tending to Infinity

Okay, maybe the mere word infinity turns you off. Well, think of it this way. When you move along the real number line starting from the origin and go right, you pass the numbers 1, 2, 3, 4… If you pass further, you will encounter bigger numbers: a thousand, a million, a billion… Well, what if you went all the way forever? That’s infinity.

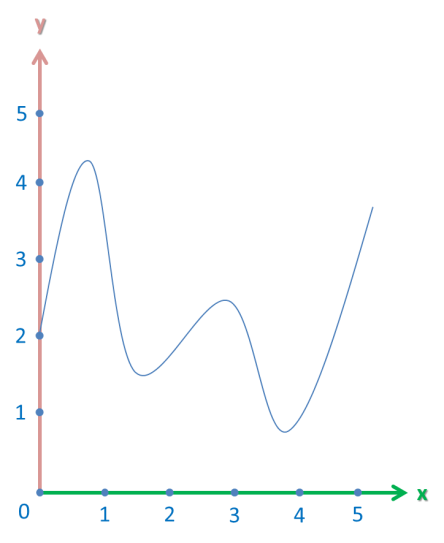
So, let’s take a look at the following graph:

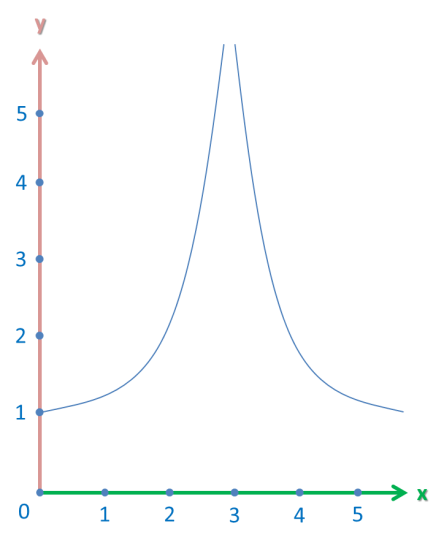
We want to find the limit of this graph as x approaches 3 from both sides.

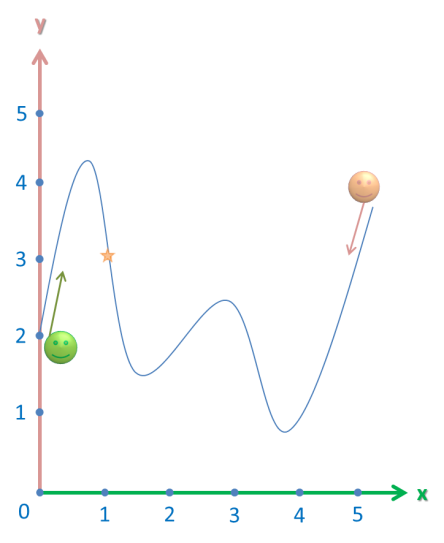
Now, you probably remember what we do when we encounter limits – we imagine two people and a roller coaster ride:

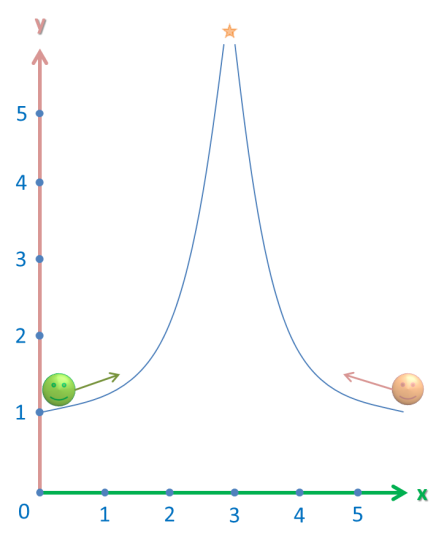
However, this graph has a vertical asymptote at the point x = 3. This is just a fancy line for a vertical line that the graph approaches, but never actually reaches.

That means that both people will never reach the meeting point, since I just said that the graph never actually reaches it. So, what is the limit at that point?

Let’s imagine that the meeting point is a point – infinity. So both people are heading toward that point, albeit forever. That means that the graph tends to infinity at that point, or:

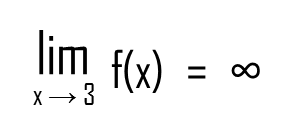
However, this is only one school of thought. Other mathematicians have decided that since infinity is not a defined point, the graph doesn’t even have a limit there. It’s up to you to decide, but now you know that the above situation is rather equivocal. However, both representations are correct – the limit-to-infinity representation and the limit-is-undefined one.

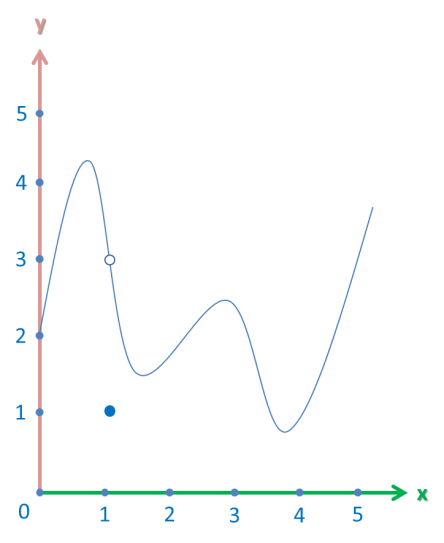
And, to close off the discussion on limits, one final graph:

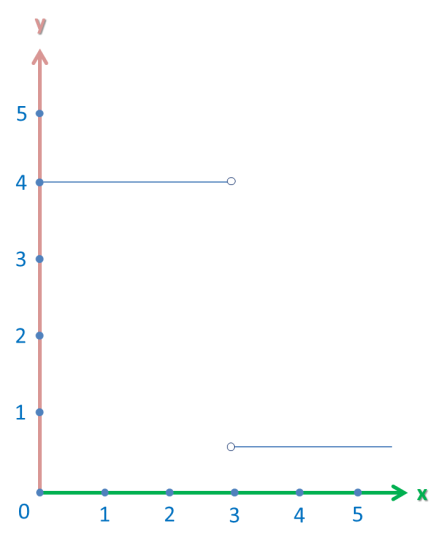
This graph isn’t defined at the point x = 3. What is the limit of the function as it approaches 3 from the left; from the right; from both sides?

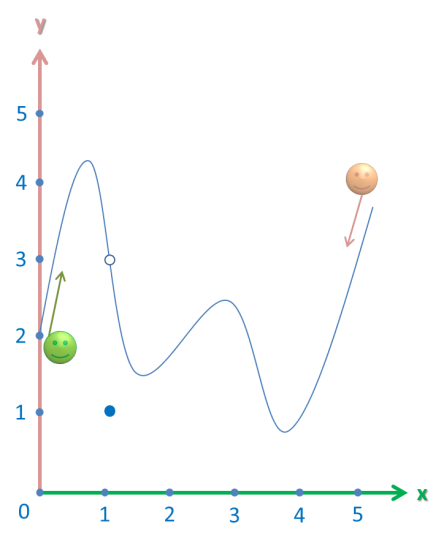
Now this question is a bit more complicated than our previous graph. However, our faithful friends come to our assitance:

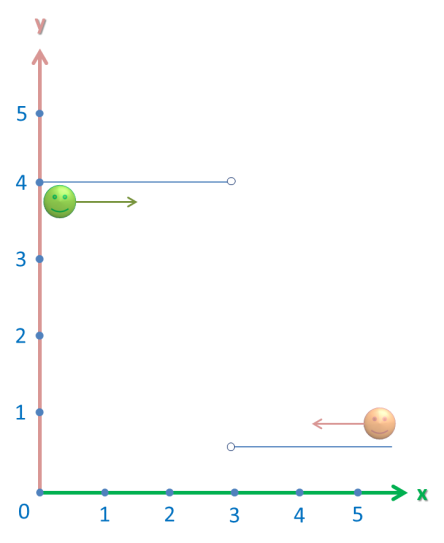
When the person in green (on the left) reaches the meeting point, he says that it’s located at the y-coordinate of 4.

However, the person on the right reaches the meeting point and disagrees. “It’s located at y-coordinate of 1″, he says.

Who’s right? Well, both of them. The limit from the left and the right are different, however, they are limits. (Again, it doesn’t matter if the function is defined there or not. It’s just how the function looks).

Let’s write it in mathematical language:

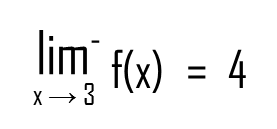
The minus sign on top of the lim simply means that x is approaching 3 from the left.

And from the right:

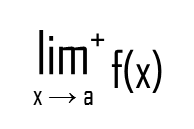
I guess you got the meaning of the plus sign. Here, x approaches 3 from the right.

However, the two limits are different. Which do we choose for the from-both-sides limit?

Well, it’s simple. No calculations, no advanced techniques. If the two limits aren’t equal, the function doesn’t have a from-both-sides limit. It’s undefined.

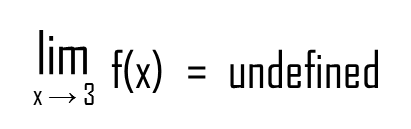
So, we’ve analyzed our fourth function and with this, I conclude this chapter on limits.

Any questions / tips / suggestions are welcome in the comments, as usual.

Until then,
Vladimirr Petrunko

Limits Demystified (Part 1)

Welcome back! It’s been a long while since I last wrote a post here… Today I’ll delve into the realm of calculus! One of the reasons for this decision is the “calculus-o-phobia” that surrounds modern students. I’d like to examine the basic tenets of calculus step by step and show that it’s really that easy!

As always, I won’t use textbook definitions or complicated formulas, just layman’s terms. However, this blog post is a bit lengthy so, if you like, you might want to tackle it in several sittings. So, are you ready?

Let’s start with a function:

Let’s find the limit of this function as the variable x approaches 1.

To do this, let’s imagine two people approaching the x-value of 1 (the “meeting point”) from opposite ends of the graph along the function like on a roller coaster ride. The following illustration shows what I mean:

Those two people just go with the flow. They don’t know how the function was defined – whether it’s a quadratic, cubic equation or a piecewise graph. They simply slide along the waves of the graph, ignorant of the mathematics behind this.

When the person on the left (in green) reaches the meeting point, he tells the y-coordinate of the point (in this case 3). To rephrase this in mathematical terms,

The limit of our function,
as x approaches 1 from the left,
is 3.

Note the key words – from the left. For now, we don’t care about the part of the graph to the right of the meeting point. We’re only interested in the left part.

The person on the right (in orange) does the same. Since the graph is continuous, he also finds that the y-coordinate is 3. Or,

The limit of our function,
as x approaches 1 from the right,
is 3.

Now, if the limit from the left and right at a given point are equal, then we say that the function has a limit at the point. So, according to this definition,

The limit of our function,
as x approaches 1,
is 3.

Which basically means: the y-coordinate of the meeting point (located at x = 1) of two people, arriving from opposite ends of the function, travelling along its graph, is 3.

You may have noticed that the value of the function at our meeting point is also 3. That’s not surprising, since our function is continuous and it doesn’t really matter whether we take the y-coordinate of the meeting point directly or arrive at the point from opposite ends of the graph.

Or does it?

Let’s take this function:

It’s almost the same as the previous function. However, unlike in the previous example, our smooth graph has a discontinuity at our meeting point. The function is defined there, though, but is equal to 1 instead of 3.

However, when we ask our two faithful friends to come together from opposite ends of the graph, we notice that they both say that the x-coordinate of their meeting place is 3. Just as before, they take a roller coaster ride:

They have absolutely no way of knowing that someone “removed” the point (1, 3) from the list (x, y) coordinates of the graph. Again, they don’t know how the function is defined. They simple ride the graph like a roller coaster.

But when they come to the meeting point, they notice something weird… The function isn’t defined at 3, it’s defined at 1. However, the function still has a limit there, and – more importantly – the limit is still equal to 3.

Just a bit of Mathematical notation…

I haven’t used a single formula yet in my blog post (and that’s good, in fact). I guess, just for the sake of mathematics, I need to show you how to write a limit formally. You won’t be rambling about people and roller coasters in Calculus class. I mean, you might do that, but it’s only for your own understanding. Here’s how you would write it on paper:

Which just means, as x approaches 1 from both sides, the y-coordinate approaches 3.

In the next blog post I’ll take a look at several other kinds of limits – limits that tend to infinity and limits that do not exist.

Until then,

Vladimirr

 

Moving to a Different Format

Hello, guys! Sorry I’ve not posted a while. Y’know, I’ve decided to take a big step in the growth of my blog, and from now on the vast majority of my blog posts will be in a video format. I have a playlist on my YouTube channel dedicated to mathematics, I’ll be uploading my math videos there.

I haven’t forgotten about matrices, I plan to make several videos about that soon. I believe that complicated topics like matrices merit their own videos, because it’s kinda difficult to explain the intricacies of advanced math in text.

Here’s my first video, where I explain a very simple way to help you remember the values of sine and cosine of 30, 45 and 60 degrees – the main angles you’ll find in geometry and trigonometry: https://www.youtube.com/watch?v=7qxfxUkpmcc Hope you like it!

See you soon!

The Lattice: An Easier and Cheaper Way to do Multiplication

Hello, guys! Been a while since my last post… Anyway, here I am today explaining a method of multiplication known as the “lattice“. It is different from the traditional “school” way of multiplying, and, in many respects, better. First I’ll tell you about the method, then I’ll explain all its perks.

Let’s multiply 3291 by 53 . We’ll proceed as follows.

• Let’s create a small grid (table), just large enough to put one number alongside horizontally, and the other number alongside vertically. So, we need as many columns as there are digits in the first number, and as many rows as digits in the second number. Let me illustrate what I mean:

• Next – we put the two numbers as I mentioned before – one on top, the other on the right, like so:

• So far, so good! Now we draw diagonal lines in the bottom-left direction, starting from all the top and right edges of the grid:

• Only two steps left to go! Let’s review what we’ve done. Now, we have 8 cells in our grid. Each cell, therefore, is divided into two halves by our diagonal lines. Now here’s what we do. Think of each cell as the intersection of two digits. For instance, the top-left cell is, actually, the intersection of the digit “3” and the digit “5”. So, for every such cell, we put inside of it the product of the two digits – one on top of the cell, the other on the right of it. I’ll explain how it looks:

If the product consists of two digits, we put the first one in the upper part of the cell; and the second one – in the lower. Otherwise, we just put the number in the lower part of the cell.

Let’s take an example. The number “9” from 3291 and the number “5” from 5  intersect at a specific cell in the grid. What is the product of “9” and “5”? Well, 45. So we put that in the target cell, with the first digit on top and the second on bottom.

We’re almost done. Now comes the last step. Here’s the picture, I’ll explain how to do this step in just a bit.

• Now comes the addition part! For this step, imagine each two adjacent diagonal lines as creating a “corridor” between them, comprised of numbers. For example, the right-most “corridor” consists only of the number “3”, and the next one (moving left) – of the numbers “5” and “7”.

Can you see the spaces on the left and bottom of the grid, right underneath the “corridors”? Well, actually, a digit is supposed to go into each of these spaces, as you’ll see next.

Starting from the right-most “corridor”, we take the sum of all the digits there, and put that in the space underneath. In this case, we only have a “3”.

Then, we take a look at the corridor located to the immediate left. It contains the numbers “5” and “7”. Since 5 + 7 = 12, we know that we should put that underneath.

But wait! “12” has two digits. What are we to do? Just remember back to the classical addition. When you have an excess place value, you simply carry. So, carry the “1” over to the left corridor (you can see a small “1” above in the third corridor from the right). And when you’ll consider the sum of the digits in that corridor, you’ll have to consider that carried “1”, too.

And we go on, right up to the very last (left-most) corridor. Then we read our answer from left-top to bottom. So,

3291 * 53 = 174423

This blog post sure was long! I hope the illustrations helped you a bit. Feel free to comment if you didn’t get a particular step (although I tried to explain them as clearly and as memorably as possible). Before we part, though, I’ll tell you why I’m teaching you this method when you have your old-school “classic” multiplication. Here are the benefits of the lattice way:

1. Ease. In the lattice method, we only need to remember two operations: multiplying 2 one-digit numbers (what you’ve learned in elementary school) and performing traditional addition (what you’ve also learned early on). When we do traditional multiplication, we have to remember all sorts of things, when to carry, what to multiply and add with what… In other words, a complete hodge-podge.
2. Speed. It’s way faster to multiply using this method, because you don’t need to remember anything. Just perform one operation at a time.

One more perk of this method is that, if you got your answer wrong, you know exactly what is your mistake. You only have two of them: wrong one-digit multiplication or wrong addition. You know what to work upon. On the other hand, in the traditional scheme, you don’t know where exactly you made a mistake, and so, you need to plod painstakingly through the whole history of operations.

I hope you found this post interesting and informative! Stay tuned for more!