Welcome back! It’s been a long while since I last wrote a post here… Today I’ll delve into the realm of calculus! One of the reasons for this decision is the “calculus-o-phobia” that surrounds modern students. I’d like to examine the basic tenets of calculus step by step and show that it’s really that easy!
As always, I won’t use textbook definitions or complicated formulas, just layman’s terms. However, this blog post is a bit lengthy so, if you like, you might want to tackle it in several sittings. So, are you ready?
Let’s start with a function: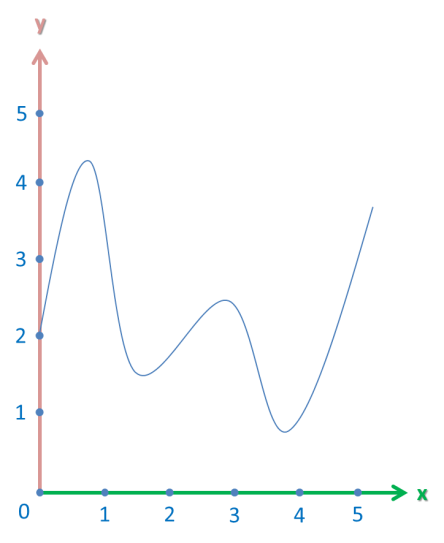
Let’s find the limit of this function as the variable x approaches 1.
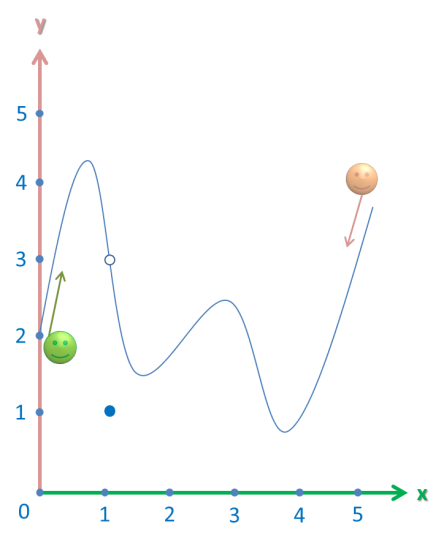
To do this, let’s imagine two people approaching the x-value of 1 (the “meeting point”) from opposite ends of the graph along the function like on a roller coaster ride. The following illustration shows what I mean:
Those two people just go with the flow. They don’t know how the function was defined – whether it’s a quadratic, cubic equation or a piecewise graph. They simply slide along the waves of the graph, ignorant of the mathematics behind this.
When the person on the left (in green) reaches the meeting point, he tells the y-coordinate of the point (in this case 3). To rephrase this in mathematical terms,
The limit of our function,
as x approaches 1 from the left,
is 3.
Note the key words – from the left. For now, we don’t care about the part of the graph to the right of the meeting point. We’re only interested in the left part.
The person on the right (in orange) does the same. Since the graph is continuous, he also finds that the y-coordinate is 3. Or,
The limit of our function,
as x approaches 1 from the right,
is 3.
Now, if the limit from the left and right at a given point are equal, then we say that the function has a limit at the point. So, according to this definition,
The limit of our function,
as x approaches 1,
is 3.
Which basically means: the y-coordinate of the meeting point (located at x = 1) of two people, arriving from opposite ends of the function, travelling along its graph, is 3.
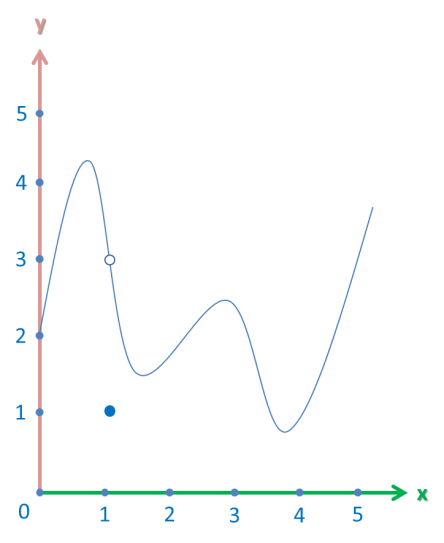
You may have noticed that the value of the function at our meeting point is also 3. That’s not surprising, since our function is continuous and it doesn’t really matter whether we take the y-coordinate of the meeting point directly or arrive at the point from opposite ends of the graph.
Or does it?
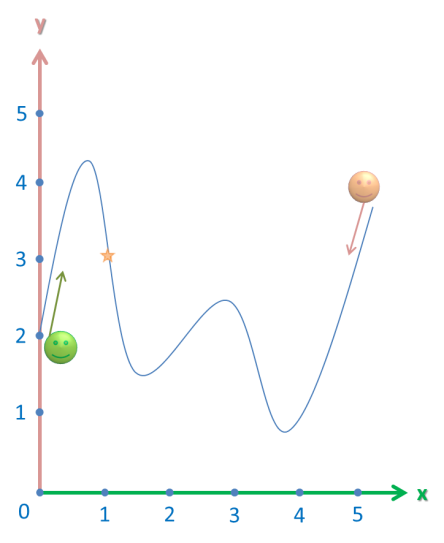
Let’s take this function:
It’s almost the same as the previous function. However, unlike in the previous example, our smooth graph has a discontinuity at our meeting point. The function is defined there, though, but is equal to 1 instead of 3.
However, when we ask our two faithful friends to come together from opposite ends of the graph, we notice that they both say that the x-coordinate of their meeting place is 3. Just as before, they take a roller coaster ride:
They have absolutely no way of knowing that someone “removed” the point (1, 3) from the list (x, y) coordinates of the graph. Again, they don’t know how the function is defined. They simple ride the graph like a roller coaster.
But when they come to the meeting point, they notice something weird… The function isn’t defined at 3, it’s defined at 1. However, the function still has a limit there, and – more importantly – the limit is still equal to 3.
Just a bit of Mathematical notation…
I haven’t used a single formula yet in my blog post (and that’s good, in fact). I guess, just for the sake of mathematics, I need to show you how to write a limit formally. You won’t be rambling about people and roller coasters in Calculus class. I mean, you might do that, but it’s only for your own understanding. Here’s how you would write it on paper:
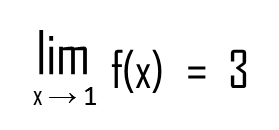
Which just means, as x approaches 1 from both sides, the y-coordinate approaches 3.
In the next blog post I’ll take a look at several other kinds of limits – limits that tend to infinity and limits that do not exist.
Until then,
Vladimirr