All images in this blog post taken from Google.
No doubt you have heard of the terms smooth and continuous when referring to functions. In this blog post, I’ll try to explain what these terms really mean; as usual, in the most informal language possible.
A continuous function is a function that you can trace with a pencil without lifting it off the paper. This is a continuous function:
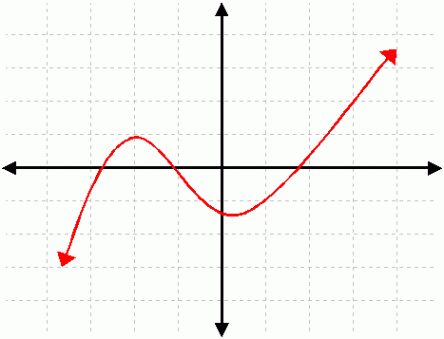
Now, if at least one of the following are true, the function is not continuous:
- At some point, you have to lift your pencil and move it to some other spot on the function to continue the movement,
- At some point on the graph, the function is not defined (it has a hole).
Smoothness is a similar, but not identical, concept. It is closely related to the concept of derivatives that I mentioned in my post Derivatives Demystified, so I’ll be leveraging that post to help us understand smoothness.
Basically, for a function to classify as smooth, it should have a derivative at all points of the graph. I won’t go into the calculus definition (I might scare you out of calculus altogether); I’ll instead use the analogy I gave you in the post above.
Here’s an example of a function that is not smooth:
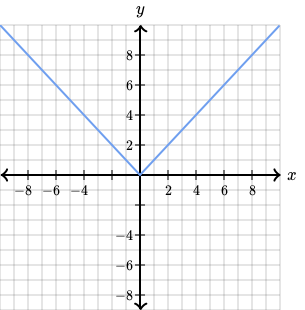
That’s the familiar absolute value function:
y = |x|
Why is this function not smooth? Well, let’s consider the point x = 0.
Graphically, this function has a steep turn at this point.
Analytically, this means that the function has no derivative at this point and, consequently, is not smooth.
Why is that?
Let’s say that we’re moving from the far left of the function to the far right and examine the derivative of the function at each point as we pass through it. I hope that by now, you remember that the derivative is just the slope of the function at the point of interest. Nothing advanced. Just easy high school algebra.
We find that for negative values of x, the derivative of the function is -1.
However, for positive values of x, the derivative is +1.
We cannot derive a formula that can calculate the derivative at any point. If we use -1 as the formula, we will get the wrong answer for all positive values of x. If we use +1 as the formula, we will be mistaken on all negative values. Any attempts to find any relationships between y and x don’t work, either.
So, the function isn’t smooth.
Now that we can recognize a function that is not smooth, can we just call it a day and say that all other functions are smooth?
Well, not really…
You see, smoothness is not a black-and-white concept. You cannot say that a function is either smooth or not. Mathematicians refer to so-called degrees of smoothness. That will be the topic of our next blog post.
Until then!