Welcome back! Today I’m returning with a new post on calculus, this time concerning derivatives. If you’ve read my series on limits, I hope you realized that calculus isn’t that scary, after all; in fact, it’s fun and exciting!
Let’s start with a quick talk on slopes of linear equations. You probably know from algebra that the process of determining the slope of a line is very easy. You simply select any interval and divide the vertical change (a.k.a rise) by the horizontal change (a.k.a. run). I illustrated this below:
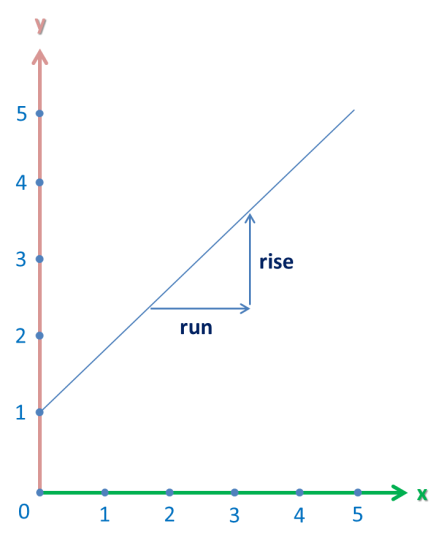
One crucial detail is that the choice of the interval doesn’t matter. The slope of a line will remain the same whether you choose the whole range (e.g. from -∞ to ∞) or a small interval (e.g. from -1 to 2).
How about if we shift this definition of a slope to other graphs. Let’s take parabolas, for example. We can take an interval on this parabola and use the formula above. So, apparently it’s easy and it works!
Or does it?
Unlike linear equations, the slope of parabolas constantly changes. I illustrated one example below:
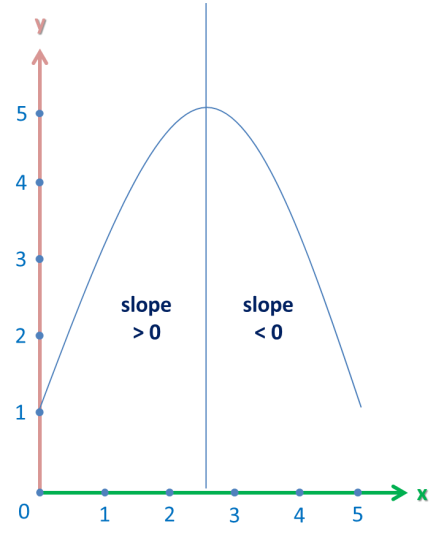
If you take an interval from the left half, the slope will be positive. However, intervals from the right have will have a negative slope.
So, that means that slopes of non-linear equations make no sense?
Well, let’s loosen the definition a bit.
Let’s represent the slope not by a number, but by a function. This function will tell us the slope of a graph at a particular point. Thus, even though all points on the graph will have different slopes, the slope operation suddenly makes sense.
And this function is called the derivative and is denoted f'(x), read “f prime of x”.
I’ll examine methods of calculating the derivative of functions in subsequent posts, but now I’ll give you a quick example.
The derivative of the quadratic function x2 is 2x. What does that mean?
Well, that means we can calculate the slope of x2 at any point just by plugging in the x-coordinate into 2x, the derivative.
For example, the slope of x2 at x = 3 is:
f'(3) = 2 * 3 = 6
and the slope at x = -5 is:
f'(-5) = 2 * -5 = -10
It’s really that easy!
Now, you might wonder, do linear functions have derivatives? Well, turns out they do! The derivative of linear functions is just a constant and is equal to the slope of the line.
So, the slope of the linear function 5x at the point x = 7 is:
f'(7) = 5
So, the derivative (a.k.a. slope) of a line doesn’t depend on the point, which rephrases what I said earlier in the post.
I hope you found this post informative and fun to read. If you have any questions or suggestions, feel free to comment.
Next time I’ll probably return with another calculus post. You may think that the easy-going nature of my posts is due to the fact that limits and derivatives are introductory material, but if you have the attitude, you’ll breeze through all of calculus easily 🙂
Until then,
Vladimirr Petrunko