Mandelbrot Sets: The Beauty of Fractals

Hello again! To-day I’d like to talk about another area of applied mathematics – fractals, and more specifically – Mandelbrot sets.

To begin with, Mandelbrot sets are just that – sets. A set is just a group of numbers. For instance, the set of even numbers is:

{-Infinity, ..., -4, -2, 0, 2, 4, ..., Infinity}

And the set of numbers either divisible by 2 or 3 is:

{-Infinity, ..., -6, -4, -3, -2, 0, 2, 3, 4, 6, ..., Infinity}

Now let’s plot the numbers in the set on a real number line. (Obviously, we can’t plot all the numbers, but let’s do a small portion of them).

We’ll color the points that we’ve plotted black and leave the others white.

So, in our second example, the coloring goes as follows:

• -6: black
• -5: white
• -4: black
• -3: black
• -2: black
• -1: white

The Mandelbrot set is constructed the exact same way, except for one crucial difference: the set is in two dimensions. This is because the Mandelbrot set consists of complex numbers, which consist of a real part (on the x-axis) and an imaginary part (on the y-axis). The numbers in the set are colored black, the ones outside the set remain white.

To make a long story short, we get the following:

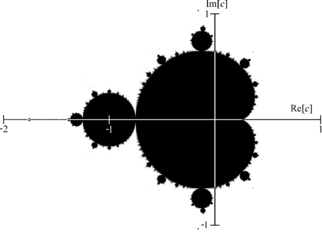
What’s amazing is that the set is extremely accurate, so if we zoom in on any part of the set, we still get a clear image. This property is a typical characteristic of fractals – we can zoom in indefinitely and produce ever more interesting patterns.

But, we haven’t answered one question: What is the set?

It’s much easier than you think. Let’s take the function:

zn+1 = (zn)2 + c

where c is the complex number under question.

So, how do we determine whether a complex number c is in the set or not? We start with:

z0 = 0

and we apply the iteration repeatedly, in other words, we calculate the values of z1, z2, z3, .... If the value tends towards infinity, then c is not in the set. Otherwise, it is.

Let’s take two examples: 1 and -1.

z0 = 0;
z1 = 02 + 1 = 1
z2 = 12 + 1 = 2
z3 = 22 + 1 = 5
z4 = 52 + 1 = 26
z5 = 262 + 1 = 677
...

So, 1 is not in the set, as the result of the function tends toward infinity.

How about -1? Let’s see…

z0 = 0;
z1 = 02 + (-1) = -1;
z2 = -12 + (-1) = 0;
z3 = 02 + (-1) = -1;
z4 = -12 + (-1) = 0;
z5 = 02 + (-1) = -1;
...

So, -1 is in the Mandelbrot set, as it does not tend toward infinity.

Just a bit of terminology here: if the values in a set tend toward infinity, it is unbounded. Hence, the results from applying the function on -1:

1, 2, 5, 26, 677, ...

represent an unbounded set.

And if the values in a set do not tend toward infinity, it is bounded. Our second set of results,

-1, 0, -1, 0, -1, ...

is bounded.

This is it! It’s that easy!

Sequel

You may have noticed that many Mandelbrot set images are not black and white, but colorful ones. Well, the principle behind that is also easy: we color each point in the set depending on how fast the values we get from that point tend toward infinity. This work is difficult (read: impossible) to do by hand, so it is usually done in a computer program, resulting in images like the following (slideshow!):

This slideshow requires JavaScript.

Thanks for reading! I hope you’ll appreciate the beauty and intricacies of the Mandelbrot set along with this blog post! Stay tuned for more!

“Instant Multiplication” tricks

It’s been a long while since I posted something on my blog… However, welcome back for another math trick! This one is pretty universal; with it you can multiply several-digit numbers without a calculator. This method works best with two-digit numbers, however with practice you’ll learn to apply it to several-digit numbers as well.

Let me show you the essence of this method first, and then we’ll take a look at an example. Also, since this blog is designed to make everything crystal clear, I’ll explain not only the method itself but the algebraic logic behind it. I mean, it’s much easier to learn something if you understand how it works, internally.

To multiply two several-digit numbers, you multiply each of its place values by each other. If you’ve heard of the FOIL method to expand a polynomial, the principle is similar. We multiply the units of the first number by all the place values (in turn) of the second number, then we do the same with the tens, the hundreds and so on. All the intermediate values we get in the process are added up.

Here’s an example to clarify my point:

93 * 671 = ?

First let’s pick out the shorter number, in this case 93. It’s not necessary, but it’s more comfortable to put the shorter number first.

Let’s multiply the units of the first number by all the place values, in turn, of the second number, and add the intermediate values:

3 * 600 + 3 * 70 + 3 * 1

I just “disconnected” the larger number into its place values and multiplied them by the units of the first number. Adding those results together, we get:

3 * 600 + 3 * 70 + 3 * 1 =
1800 + 210 + 3 =
2013

Now let’s multiply the tens of the first number by all the place values of the second number. The exact same operation, but performed on the tens, rather than the units, of the first number.

90 * 600 + 90 * 70 + 90 * 1 =
54000 + 6300 + 90 =
60390

Notice that whenever we take a place value, we take both its numerical representation and however many zeroes would go after it. In other words, if we take the tens place value, we place one zero after it; the hundreds place value – two zeroes, and so on.

Now we’re done, since the first number only has two place values. Now we need to add all our results:

2013 + 60390 = 62403

In this method, we basically only need to perform two kinds of operations:

1. Multiplication of one-digit numbers. You may know that when one number has a bunch of zeroes and we need to multiply it by another number, we can simply ignore the zeroes while calculating and append them to the result.
2. Addition. Your addition skills will definitely come in handy here. You could do this on pen and paper, on in your head. Typically, the smaller the number, the faster you could do the addition.

Let’s examine one more example.

98 * 12 = ?

Let’s multiply the units of the first number by all the place values of the second number:

8 * 10 + 8 * 2 =
80 + 16 = 96

And multiplying the tens of the first number by all the place values of the second number:

90 * 10 + 90 * 2 =
900 + 180 = 1080

Adding both of those results together gives:

1080 + 96 = 1176

I believe that this method works best with two-digit numbers. Then the whole calculation can be performed mentally. If the number is larger, it may require some practice.

And one more point. Both of the examples we’ve been dealing with in this blog post only had two intermediate results, which we added up to get the final number. That was only because the first number had two place values. If the first number had, say, 4 place values, we would have 4 intermediate results.

Hope this blog post helped you!

 

Mathematicians on Quora

Welcome again to Algebra Demystified! In this blog post I’ll deviate from my normal strategy, whence I pick a topic of discussion and explain it in a blog post.

I believe I’ve mentioned the Quora forum in a previous blog post on geometric sequences, but, in case you haven’t heard of Quora, it’s just a handy question-and-answer forum. This post is mostly meant for those who have already joined Quora (however, even if you haven’t, it’s very easy to do it).

There are a number of topics (and, for that matter, writers) that have excellent answers on math and similar topics, like physics and chemistry. There are several of them that are worth reading. Here they are:

1. Alon Amit – he writes on the more basic and at the same time puzzling aspects of math, such as problem solving and number theory. He also has a number of answers on arithmetic and algebra too.
2. Richard Muller. In addition to rich math insights, he also is a physics professor and so has a number of great answers on this topic. I think he is one of the leading authorities on physics of our time, concerning issues as profound and diverse as relativity, gravity waves, time and dark matter.
3. Senia Sheydvasser. He writes on the fundamental aspects of math, like proofs and algebra, but at the same time he touches upon calculus and the various math disciplines associated with it.

That wasn’t much, but these people have literally hundreds and hundreds of answers worth viewing! In addition, you shouldn’t have to be signed in to Quora in order to read others’ answers. It’s only to issue your own questions and answers that you have to be a user by signing in.

Best of luck!

Extraneous Solutions Demystified

Usually, when you solve any equation, you either find a solution (or two, or three, or more) or prove that the equation doesn’t have any solutions. Both outcomes are perfectly okay, although you won’t be given many equations that don’t have solutions, since it’s usually easier to prove that an equation doesn’t have solutions than to seek them out manually.

But, whether you’re a struggling student or a top-class mathematician, you shouldn’t stop once you’ve solved an equation. You must always check your solution. Now, the obvious reason is that you may have made a mistake and you may get the wrong solution (or even the wrong number of solutions). But there’s another reason.

Even if you have done every single operation correctly, there’s still a risk (especially in equations with a degree of 2 or greater) that you introduced an extraneous solutions. Extraneous solutions are solutions that you get after a series of legal manipulations of the original equation, but don’t fit the original equation at all! Here are some cases that can cause potential extraneous solutions:

1. Multiplying by 0 (or by a variable that, in the end, equals 0). When you’re multiplying by 0, you’re increasing the solution set of the equation. And, though you won’t multiply an equation flat out by the number 0, you may find yourself multiplying by a variable, which turns out to be equal to 0.
2. Rational expressions. When we have a variable in the denominator, there’s a chance that it evaluates to 0. Since we can’t divide by 0, the whole expression turns out to be illegal. Here’s a rule of thumb: when you have rational expressions, always check for extraneous variables. Just as a reminder, rational expressions are expressions that represent a quotient of two polynomials.

Remember that extraneous solutions are not the only problem you may have when solving equations. Missing solutions are also an insidious problem – but that’s a topic for another time! Now, I’ll show you a real example involving extraneous solutions:

|4x + 10| = 6x
4x + 10 = 6x     OR     4x + 10 = -6x
2x = 10          OR     -10x = 10
x = 5            OR     x = -1

So, we’ve got two potential solutions: 5 and -1. But, we’re not done yet! We need to substitute each solution in the original equation to check whether they fit. Mind you, each operation we’ve done so far was legal (arithmetically), but that doesn’t guarantee that both (or even one) of our solutions is correct. So, let’s check the solutions one by one:

|4(5) + 10| = 6(5)
|20 + 10| = 30
|30| = 30
30 = 30

Great! The first solution works! Now let’s try the second one:

|4(-1) + 10| = 6(-1)
|-4 + 10| = -6
|6| = -6
6 = -6

Oooh… That doesn’t seem right, so we discard -1 as a potential solution. It is what we call an extraneous solution. We got it by performing legal operations on the original equation, but it still doesn’t fit, so we don’t include it in our solution list.

At times, you may find two or more solutions, and all of them might be extraneous ones! That most often happens in higher-degree equations with all sorts of complicated operations. But, usually, almost every equation you’ll be given will have at least one solution.

Hope you found this post informative! Best of luck!

Proofs Unveiled – The “End Digit”

Have you ever written an algebraic proof at school or college? Proofs have become such a widespread aspect of modern algebra and geometry that I can’t already imagine today’s curriculum without them… Nevertheless, many students regard proofs as a torture. They really are, if you don’t know how to deal with them.

To solve a proof, you need to remember one thing – proofs can be grouped in categories. There are geometric proofs and algebraic proofs, and both of them can be subdivided into more groups. Today I’ll talk about one kind of proof – the end digit proof – which is my favorite!

Here’s an example: what is the end digit of the expression 222222? Such an example is herculean unless you apply logic to it. And it’s not difficult! In fact, it’s almost as easy as you can even imagine! To solve such a problem, here’s what we’d think:

1. In the original base (the number to the left of the exponent), only the end digit matters. After all, when you multiply two numbers, only the final digit contributes to the end digit of the product. So, we need to leave off everything but the very last digit of the base. In other words, you’ve mentally simplified the problem to  2222, which is easier to think through, since you need to keep track of one digit.
2. Find the correlation between the exponent and the end digit of the answer. Let’s use small exponents, starting from 1. Then let’s try to find a relationship between the exponent and the end digit. If we do find one, then we can trace the relationship all the way to the needed exponent without physically examining every single exponent. Here’s how we’d do it:

2¹  = 2

2²  = 4

2³  = 8

2⁴  = 16

2⁵  = 32

Aha, we’ve found a cycle! It repeats itself every 4 exponents. Since at the beginning the end digit is 2 and it is the same at the end of the cycle, we can conclude that the pattern repeats every 4 steps. The sequence of end digits (starting from the exponent 1) is 2, 4, 8, 6, 2, 4, 8, 6, 2, 4, 8, 6, … The pattern keeps going on indefinitely, so we have no need to look further. We’ve found the relationship!

Now we just need to trace this pattern forward to our needed exponent – 222.

Let’s start with the exponent of 1, which correlates to an end digit of 2. Let’s add 200 to the exponent. Since 200 is a multiple of 4 (4 is the length of the cycle), the position in the cycle doesn’t change, so the exponent 201 also correlates to an end digit of 2.

Let’s add 20 to the exponent. 20 is also a multiple of 4, so an exponent of 221 still matches an exponent of 2.

Now, if we try to add more multiples of 4, we’ll exceed our initial exponent of 222. So let’s instead follow the cycle.

Since 222 is one more than 221, we’ll be one step down the cycle with an end digit of 4. So this is our answer.

To summarize, we need to:

1. Shrink the initial base to the very last digit, since only it affects the end digit of the answer,
2. Find a correlation between the exponent and the end digit, by working with small exponents (usually start with 1),
3. Find the cycle’s length,
4. Work your way to the needed exponent by repeatedly adding multiples of the cycle’s length, whenever possible.
5. Then, when you’re really close, just follow the exponent-end digit correlation until you’re done!

Hope my post helped you in some way! 🙂

How To Remember Circumference & Area – 2 Fun Mnemonics

Hello and welcome to Algebra Demystified! Today I’d like to tell you about a great mnemonic tool to remember the formulas of the area and circumference of a circle. As you know, I love mnemonics, and whenever I find a good one, I’m always posting it on my blog!

I’ll start by listing the two formulas and the legend of the symbols (what the letters mean in the formulas). Then I’ll tell you the (short) mnemonic phrases. I meant to build the suspense up to the end, but you may skip to the end if you’d like and work backwards.

C = πd

The legend goes as follows:

1. C stands for the circumference,
2. d stands for the diameter of the circle.

The diameter of a circle is the length of a line that you can draw between two points on the edge of a circle, provided you cross the center. You would do it like so:

And the formula for the area of a circle is:

A = πr2

The legend is:

1. A is the area of the circle,
2. r is the radius of the circle.

The radius is the distance from the center to any of the points on the edge. If you’d like a neater explanation, just take any of the halves of the diameter formed by the center. Both of those halves could be called a “radius”.

Now comes the mnemonic:

Cherry pies are delicious! Apple pies are too!

I left the most fun part for the end! Those two mnemonics stand for the two formulas I mentioned in this post. It’s better to remember them together, since they form a great logical blend.

Cherry (C) pies (π) are delicious (d)!

Apple (A) pies (π) are (r) too (²)!

There’s only one caveat to this mnemonic, which is not to mistake the “are” in the first sentence with a “r” in the formula. But remember, we never put radius and diameter together in any formula, since the radius and diameter of any circle can be expressed in terms of each other. In other words, if you know the radius, you can calculate the diameter by doubling the radius. And if you know the diameter, calculating the radius is no big deal: you simply divide by 2.

As always, suggestions, thanks, or just any comments are welcomed in the Comments section! Thanks and I hope that my blog post has helped you in some way! 🙂

pH Demystified

Hello, everyone! Today I’m taking a break from the normal Math direction of my blog and I’ve decided to take a look at applied Math in Chemistry. Along the way, we’ll be learning about a crucial concept in Math – which is logarithms. So, let’s get started!

Most of you know about the pH concept, which is a measure of whether a solution is acidic or basic. But the concept of what pH really is – in other words, what is the quantity that it measures – is relatively unknown.

pH – or potential hydrogen – measures the acidity of a substance in terms of the concentration of its hydrogen ions. In other words, the concentration of H⁺ ions in a substance uniquely determines its pH. In technical terms, the formula for determining the pH of any substance would be:

pH = -log10[H+]

So, we take the base-10 logarithm of the concentration of hydrogen ions, and then take the opposite of that. And we get the value of the substance’s pH.

Let me take a back step and quickly explain to you the essence of logarithms. I’m sure you have some idea of what a logarithm is, but I’ll explain to what they exactly are. I won’t indulge in the technical details, but rather explain it in a more casual way:

If you take the logarithm base x of a number y, you want to know how many times you should multiply x by itself to receive y. Obviously it won’t be an integer each and every time, because y won’t always be the perfect number. Fractional logarithms are also allowed.

So, we take the logarithm base-10 of the concentration of H⁺ ions. In other words, we’re looking for how many times you should multiply 10 by itself to reach the concentration of H⁺ ions.

After we’ve found the number, we just take the opposite of it, and we get the pH of the substance in question.

If the pH is from 0-7, the substance is acidic. Citric acid is an example of such a substance.

If the pH is 7, the substance is neutral. Pure water is an example.

If the pH is 7-14, the substance is alkaline/basic. Milk is an example.

I hope you got something from this blog post! Stay tuned for more!

How To Solve Equations Instantly (well, almost…)

Hello! In this blog post I’ll share with you a cool secret that will help you a lot in math. It goes without saying that equations are the heart of algebra, but I’m sure you’ll need them in pretty much any mathematical discipline, be it physics or chemistry, geometry or calculus. You’ll find equations pretty much wherever you go.

Let me explain to you, in this post, a neat way to solve many equations very fast. Okay, I’m deviating from the word “instantly” that I’ve used in my title, but the method I’ll teach you now will really come in handy when you’re sitting on a desk, seeing a 90-minute timer ticking nearby, with a standardized exam paper and a pen in front of you. Sounds scary? Well, many students just waste their own time on unneccessary operations. Before I’ll tell you about the innovative method, let me list one of the time-wasters.

You may know the rule that you can add (subtract, multiply, divide) any number to an equation as long as you perform the operation on both sides. Surely a familiar rule, right? Well, many students actually do the following:

1. Write the equation.
2. Write the performed operation carefully under both sides of the equation.
3. Perform the operation.
4. Rewrite the equation.
5. Repeat.

Actually, steps 2-5 are just not necessary! Why don’t people recognize that it’s possible to simply move a term or factor from one side to the other side, simply flipping the sign to the reverse? So, in other words, if you can see a +26 on one side of the equation, you can simply “move” that term to the other side, but changing it to -26, since we need to reverse the sign.

Well, enough beating around the bush, now I’ll really tell you a method that can save seconds, minutes, or even–if you count the net total–hours. Now that we’ve brushed the topic of timewasters, I hope you get that any way that works will do. Okay, if you’re in elementary school the teacher may ask you to carefully scrutinize each small procedure. But you don’t need that when you’re calculating the velocity of an object during angular rotation, right? No one even will bother looking at the details of your equation-solving process.

Before I’ll tell you about this method, I’m sorry to say that it only works on a limited subset of all equations. In order to use the method, the equation must only have one variable, and it must appear only once in the whole equation.

And if the equation doesn’t meet the criteria I posed? Well, try to transform it. The rule I mentioned earlier might help – don’t bother subtracting/adding/multiplying/dividing off both sides, just move–literally, move!–the terms (factors) from one side to the other.

Let me examine this new method on the example of the following equation:

5(x + 3) - 2 = 43

First we need to imagine the following picture. Let’s imagine a lonely variable x sitting all by itself. We need to find a way to “transform” it to the full-fledged expression on the left of the equals sign. To do that, we need to change x, one operation at a time. For instance, we might add 2 to it, or multiply it by 3, or raise it to the 6th power, but we need to do it… one… operation… at… a… time.

Let’s try it. What is the “closest” operation being performed on the variable? What is the first thing done to x? Well, it’s obvious that first we should add 3 to it.

What’s then? Well, now the expression takes the form of x + 3, since we’ve added 3 to the lonely variable x sitting all by itself. What is the next closest operation? Well, multiplication by 5. After adding 3, we multiply what we got by 5. And we get 5 (x + 3).

What’s then? Well, the only operation left is -2. We subtract 2 from the resulting expression, and thus we’ve transformed the lonely x into the full expression on the left of the equals sign.

Let’s sum up what we’ve done so far. We’ve gone from a single variable x to the whole expression on the left side of the equation. How did we do this? We applied one operation at a time, in the right order and place, to gradually increase the complexity of the expression until we’re done. Now we need to write these operations in a chain:

+3  *5  -2

(By the way, the asterisk indicates multiplication).

After we’ve completed the chain, we now reverse the chain. In other words, we “turn it upside-down”:

-2  *5  +3

Okay! Now… one step left! For each step in the chain, we need to compute its reverse. So, the reverse of, for example, -2 would be +2, the reverse of *5 would be /5, and so on. We would get the following sequence of events:

+2  /5  -3

Now… we’re set for the finale… Do you see the number on the right side of the equation? In this case, it’s 43. Now, from beginning to end, we need to apply all the operations on the newly-created list to this number–and we’ll get our answer.

43 + 2 = 45

45 / 5 = 9

9 – 3 = 6

And, sure enough, 6 is our answer!

I apologize if my post was too long. In case you didn’t get everything (or didn’t have time to read it all), here are the main points that you need to get:

1. Equations are the heart of algebra – you’ll need them practically everywhere!
2. Many students apply techniques of unneccessary length when they solve equations – they’re good for a beginner, but detrimental later, since with time people should keep track of more and more things – formulae, variables, constants, etc.
3. Do not visualize adding and subtracting (or multiplying and dividing) terms or factors on your paper unless you’re explicitly told so!
4. To solve many equations almost instantaneously (and this requires practice, believe me), use the so-called “chain” method. First, start with a single variable x. Then, slowly, recreate the whole left-hand side of the equation one operation at a time. You will then have a stack of operations. When you’re done, turn it upside down and reverse each operation in the list (if you’re adding a number, subtract it; if you’re cubing a number, take its cube root, and so on). Then apply all the operations in the new stack to the number on the right-hand side of the equation.

All this requires practice! In fact, I think this way will require even more time than usual at first. But, practice makes perfect, and I’m sure you’ll do it in the end!

How to Remember the Quadratic Formula

Hello! Sorry for the long break from my last blog posts, it was really something I shouldn’t have allowed myself given the relative success of my last few blog posts. Anyway, I’ve decided to break the ice here with a quick mnemonic tool concerning the quadratic formula.

This formula lets you solve quadratic equations, which by some are considered to be one of the difficult aspects of algebra. Some consider it to be a gibberish concatenation of as, bs and cs along with some coefficients. Yet it is crucial to the very existence of algebra and its related subroutines.

Here I take a picture of this formula:

 

And here’s a mnemonic to help you remember it. It comes in various modifications if you ask different people, but the basic version goes about like so:

A negative boy was undecided whether or not he should go to a radical party but his 2 friends who were boys went and there they met 4 amazing chicks and stayed up until 2am.

Let’s examine the various parts of this “story”:

1. A negative boy – (-b)
2. Was undecided – (+-)
3. … to a radical party – (square root symbol)
4. his 2 friends (b^2)
5. … 4 amazing chicks – (4ac)
6. stayed up until 2am – (division by 2a).

Hope this helped and stay tuned for more!